How to Read Coefficient of Linear Expansion

Introduction
Thermal linear expansion is a source of uncertainty that you lot need to consider if y'all perform dimensional and mechanical tests or calibrations.
Typically, it affects measurement results that involve length or deportation. However, it can also affect measurement results in the following categories:
- Force per unit area
- Torque
- Catamenia
- Volume
- Area
When evaluating thermal expansion, well-nigh people know to observe the coefficient of thermal linear expansion. However, many people take trouble applying it to their measurement results.
So, I decided to create a guide to teach you everything that you need to know about thermal linear expansion and how it affects your measurement results.
In this guide, you will larn:
- What is Thermal Linear Expansion
- Why Thermal Linear Expansion is Important
- When to Include Thermal Expansion in Your Budgets
- How to Reduce Thermal Expansion
- Thermal Linear Expansion Formula
- How to Calculate Thermal Linear Expansion (step by pace)
- Examples of Thermal Linear Expansion
Click here to download the thermal expansion calculator for gratuitous!
What is Thermal Linear Expansion
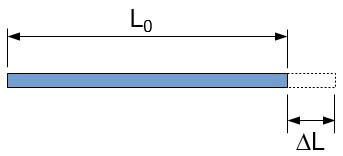
According to The Engineering ToolBox, when an object is heated or cooled, its length changes by an amount proportional to the original length and the change in temperature.
According to Merriam-Webster, thermal expansion is the increase in linear dimensions of a solid or in the book of a fluid considering of change in temperature.
Therefore, information technology is the change in the dimensional backdrop of an object when exposed to changes in temperature.
If yous perform dimensional and mechanical testing or calibration, yous may want to consider thermal expansion when estimating measurement uncertainty. Most likely, information technology affects your measurement results and should be included in your uncertainty budget.
Why is Thermal Expansion Of import
Thermal expansion is important because it can affect your measurement results. Furthermore, it can affect the quality of your customer's measurement results.
In a globe where tighter tolerances are in need, thermal expansion errors could have a meaning effect on meeting specifications.
When you neglect to consider its effects, you provide your customers with bad measurement results that could affect the quality of their products and services. Additionally, disregarding these errors can increase your gamble of encountering a false-accept or false-reject in your conformance statements.
Depending on your customer's business concern activities, bad measurement results could increase their take a chance of issues, amercement, and unplanned downtime. Even worse, it could impact the health and safety of people.
According to a contempo study by Vanson Bourne, 23% of all unplanned downtime in manufacturing is the result of human error.

It can touch on the following measurements:
- Pressure (changes in book and area)
- Torque (changes in radius)
- Flow (changes in volume and area)
- Speed/Velocity (changes in length/distance)
- Free energy (changes in length/distance)
- Book (changes in length, width, and height)
- Surface area (changes in length and width)
When to include Thermal Expansion In Your Doubtfulness Budget
You should include thermal expansion in your uncertainty budgets when:
- its upshot is considered to be pregnant, or
- the measurement outcome is not corrected for it.
Typically, thermal linear expansion doubt affects dimensional and mechanical measurement systems. However, it is not always considered in the uncertainty upkeep.
If thermal expansion contributes to five-percent (v%) or more than of the total doubtfulness, then it is considered to be pregnant and should be included in your uncertainty budget.
If the event is estimated to be less than 5%, and then it tin can exist omitted from your budgets.
If you take expansion into account when performing tests or calibrations, then yous tin omit it from your uncertainty budget. If yous do not correct for it at the fourth dimension of exam or scale, so I recommend that you include it in your uncertainty analysis.
Nevertheless, I always recommend including common sources of uncertainty in your upkeep fifty-fifty if you give it a value of naught. But make sure to include notes explaining why it was or was non considered in the analysis. This will help you and assessors understand your uncertainty budgets.
How to Reduce Thermal Expansion
There are several ways to reduce the effect of thermal expansion. You tin endeavour to:
- Reduce contact with/exposure to heat sources,
- Control the environment,
- Permit thermal stabilization, and/or
- Correct for thermal expansion
Making contact with an item can transfer your body heat to the detail causing thermal expansion. Additionally, placing an item adjacent to a heat source, heat sink, or cooling source can alter the item'due south temperature causing expansion or contraction.
If you tin reduce contact with or exposure to heat sources, you can reduce the effect of thermal expansion.
Try to avoid:
- Body heat,
- Equipment that generates oestrus,
- Windows,
- Sunlight,
- HVAC vents, and
- Objects with a unlike temperature
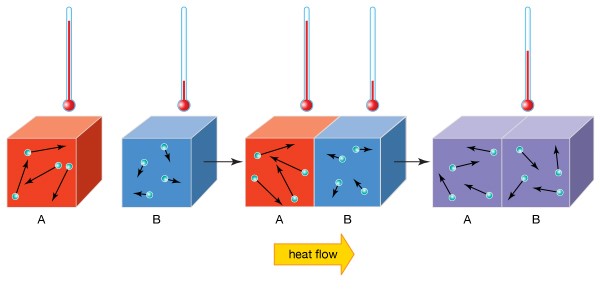
In the prototype below, you see two objects with different temperatures make contact. Heat flows from the warmer object to the cooler object (1st Law of Thermodynamics) until they achieve thermal equilibrium. The larger the temperature departure, the greater the charge per unit of estrus flow.
To reduce thermal expansion effects, avoid making contact with objects that accept different temperatures.
Another fashion to reduce thermal effects is to command the environment. A well-conditioned environment volition reduce oestrus transfer and help an item maintain a stable temperature which volition reduce thermal expansion.
Furthermore, you can minimize thermal effects by allowing an detail to thermally stabilize in the surroundings it will exist tested or calibrated. If you allow the item to achieve thermal equilibrium with the environs, it will reduce the effects of thermal expansion.
Finally, you can always correct for thermally induced errors to minimize the effect on your measurement results. Make sure that you monitor the detail'southward temperature, non just the temperature of the environment. Air temperature is bailiwick to change faster than an particular's temperature. So, monitor the particular'southward temperature or accept into consideration the textile'due south rate of thermal conduction to guess thermal furnishings due to changes in air temperature.
See How We Can Help Your Lab Get ISO/IEC 17025:2017 Accredited
- Uncertainty Budgets – let united states of america estimate doubt for you.
- Custom QMS – nosotros'll create your quality manual, procedures, lists, and forms.
- Preparation – get online training that teaches you how to estimate doubt.
Book a Call
Thermal Linear Expansion Formula
Calculating the effects of thermal linear expansion is not difficult. There are only few variables that you need to know to perform the calculation. These factors are:
- Original length,
- Coefficient of linear thermal expansion,
- Initial temperature, and
- Final temperature
It is not always easy to find the exact thermal expansion coefficient associated with the textile that you are evaluating. The best recommendation that I can give you is to contact the manufacturer of the particular you are evaluating to find the actual material composition and expansion coefficient.
Otherwise, you may accept to look upwards a reference table to notice the closest value.
Use the formula provided beneath to summate thermal linear expansion. The result tin can be used to guess the thermal effects on measurement uncertainty.
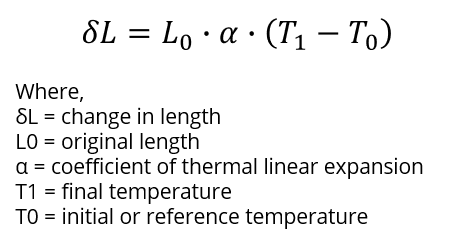
How to Calculate Thermal Linear Expansion
Follow the instructions below to calculate thermal linear expansion using the formula in the previous department.
Pace 1. Find the original length of the object
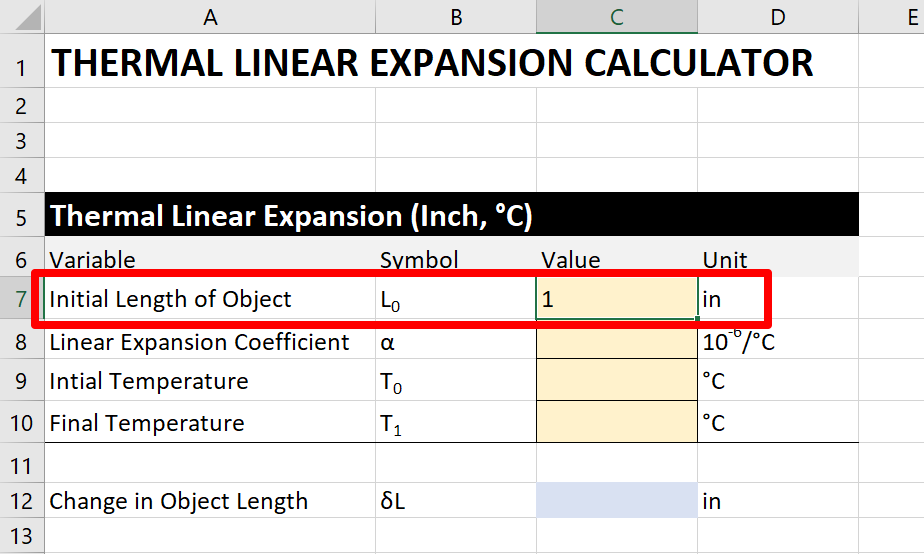
For this process, permit's estimate the thermal linear expansion of a 1 inch gauge cake.

If you download the estimator associated with this guide, enter the original length of the object. Use the image below for guidance.
Footstep ii. Discover the coefficient of thermal linear expansion
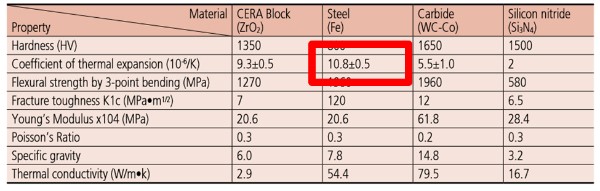
Refer to manufacturer published specifications to find the coefficient of thermal linear expansion. If yous cannot find it, try using a reference table to get an guess value.
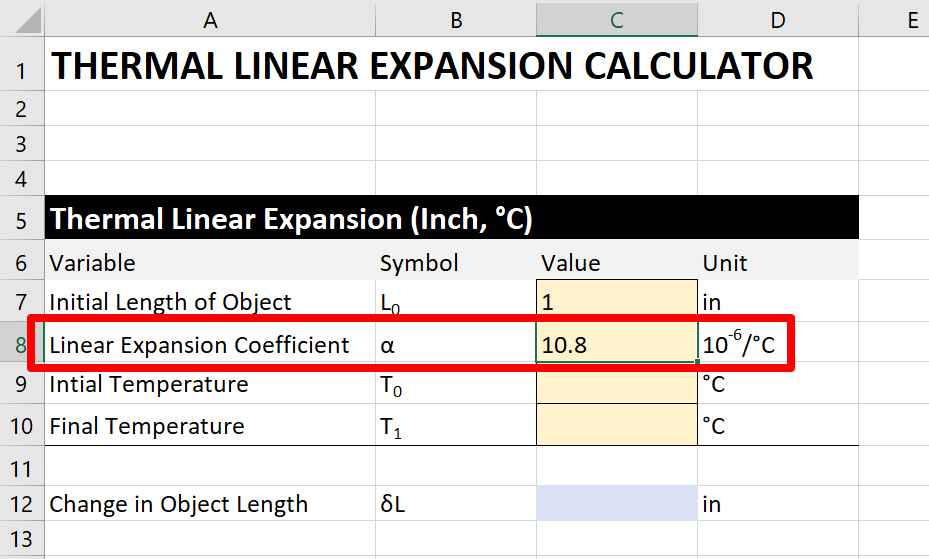
Then, enter the coefficient of thermal linear expansion into the calculator. Apply the epitome below for guidance.
Step 3. Notice the initial temperature
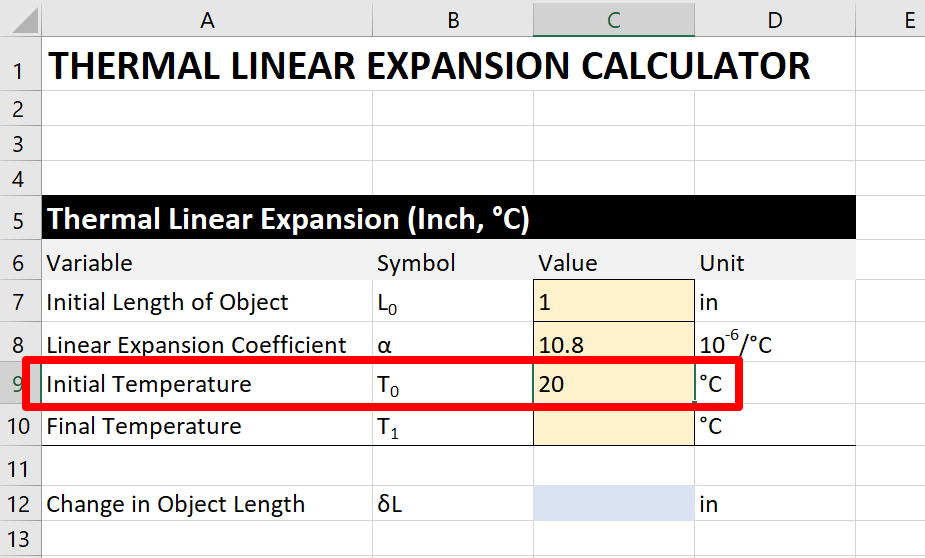
At present, monitor and record the objects temperature before you brainstorm testing or scale. This will exist the initial temperature.
So, enter the initial temperature into the calculator. Use the image below for guidance.
Step iv. Observe the final temperature
Afterward you lot have completed your exam or calibration, record the final temperature. Then, enter the concluding temperature into the reckoner. Utilise the image below for guidance.
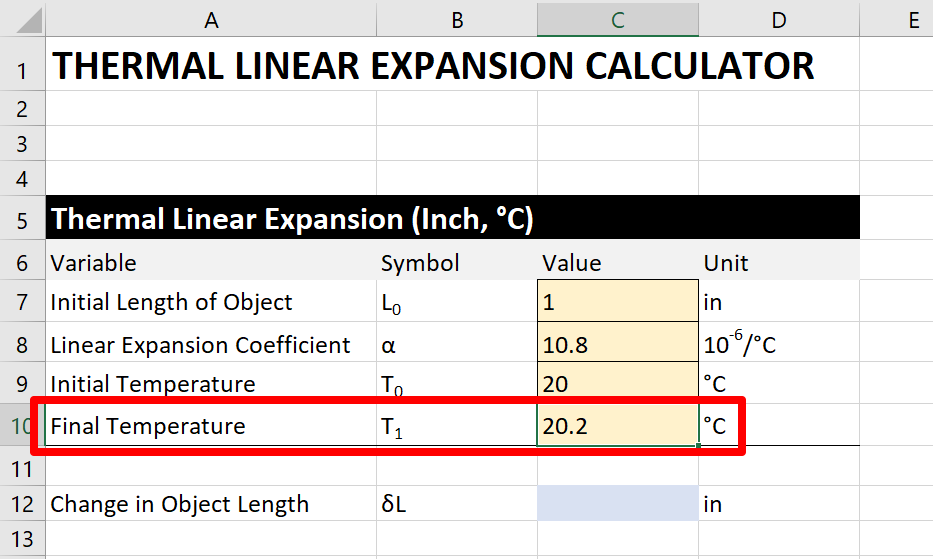
Step 5. Summate the change in length
Next, summate the thermal linear expansion using the formula in the previous section. To make the task easier, I have broken down the process co-ordinate to the order of mathematical operations.
5a. Calculate the change in temperature
To calculate the change in temperature, subtract the terminal temperature by the initial temperature.
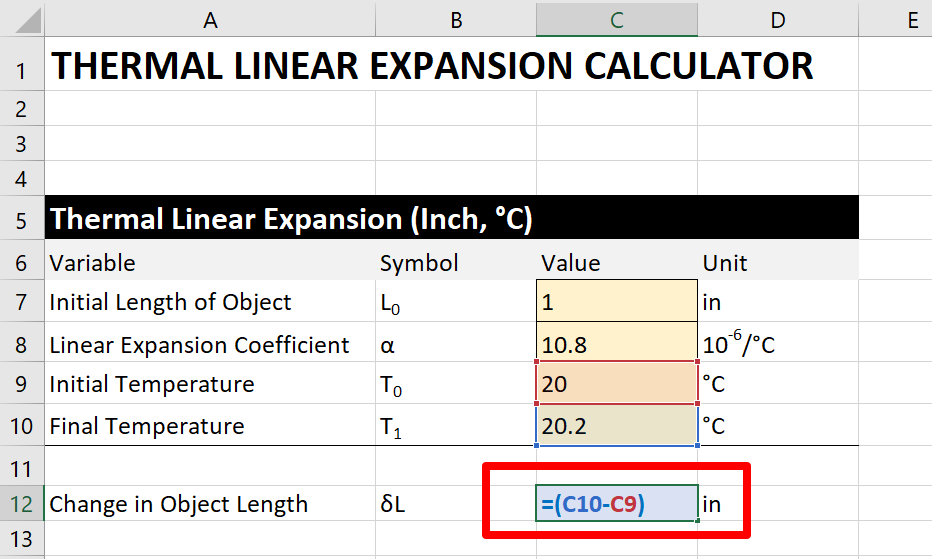
5b. Multiply past the coefficient of thermal linear expansion
Next, multiply the result from step 5a by the coefficient of thermal linear expansion.
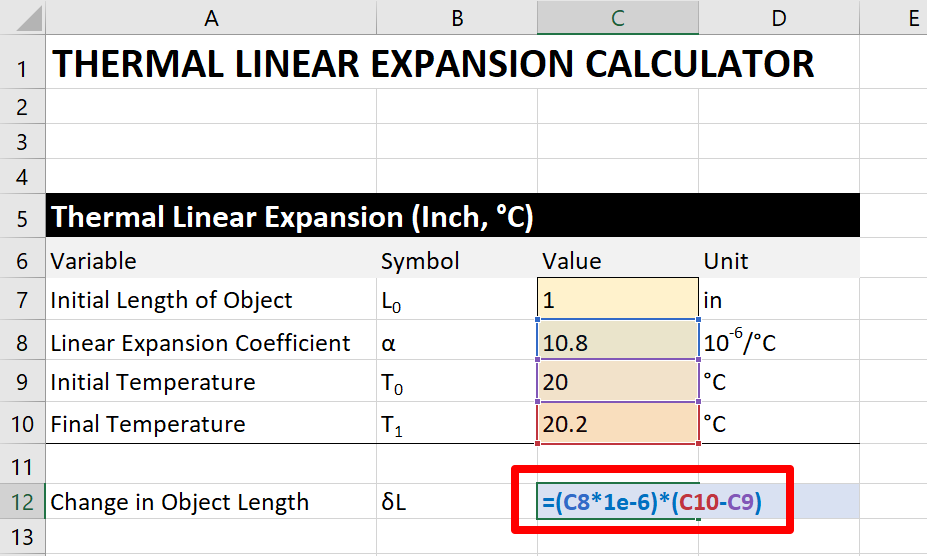
5c. Multiply by the original length
Now, multiply the consequence in pace 5b by the original length. The issue should be the alter in the object's length due to changes in temperature.
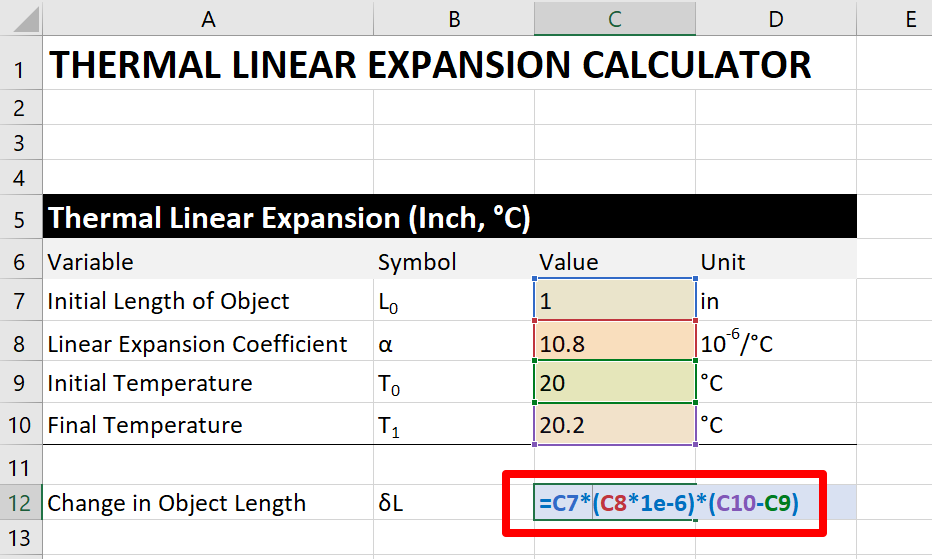
Step 6. Verify The Upshot
Finally, double cheque you piece of work and verify the result is correct.
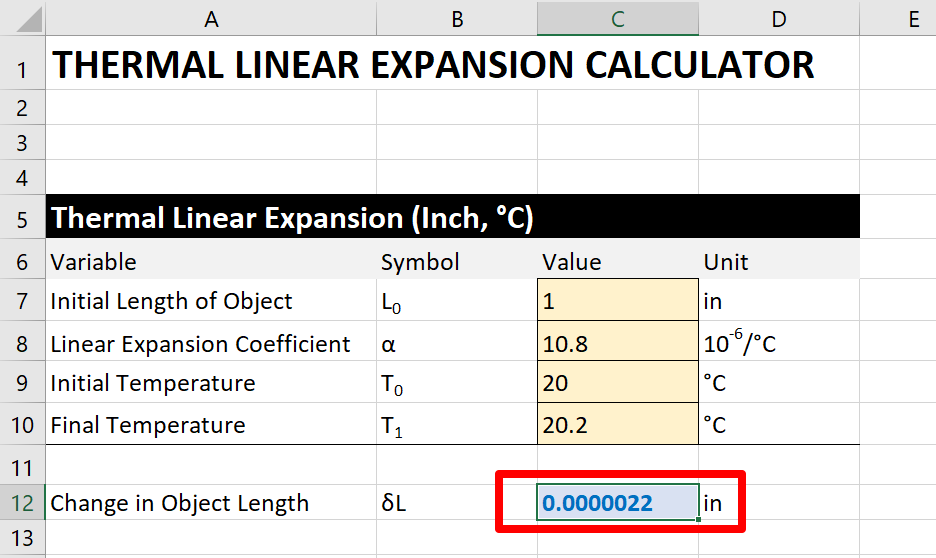
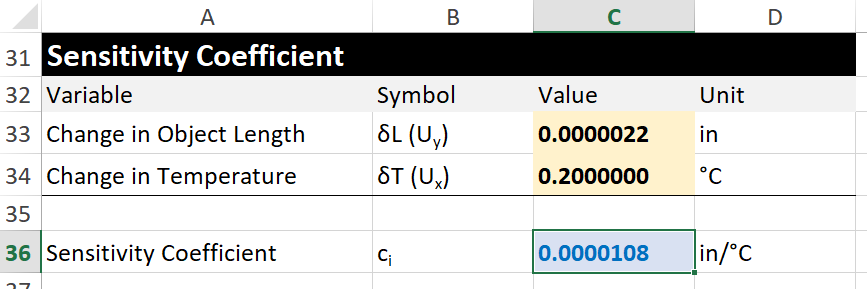
Footstep 7. Summate the Sensitivity Coefficient (Optional)
If you lot prefer to use sensitivity coefficients in your doubt budgets, split up the change in object length (Uy) past the change in temperature (Ux). This will give you lot the sensitivity coefficient.
At present you can add the sensitivity coefficient and the change in temperature to your uncertainty upkeep.
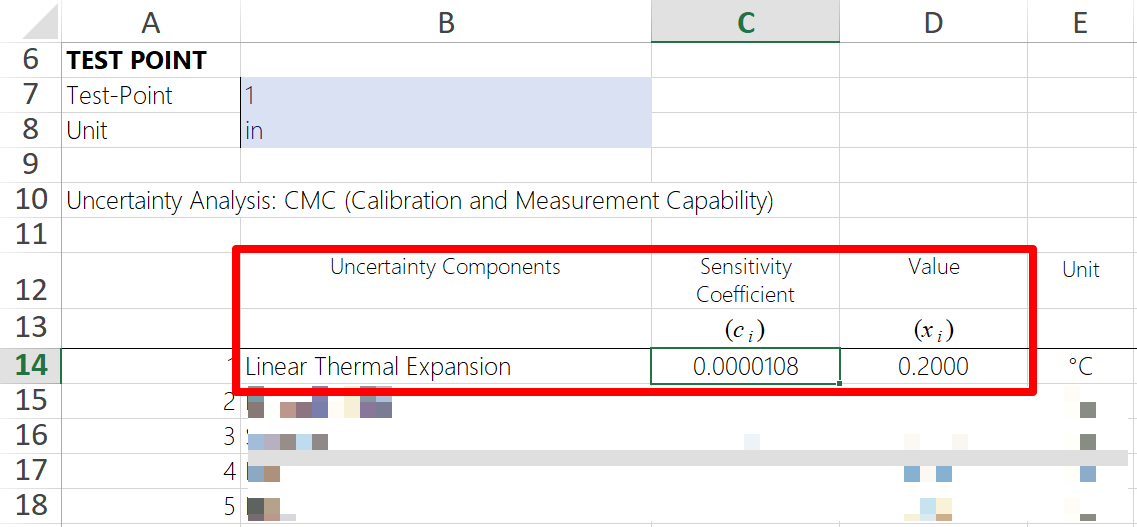
Using sensitivity coefficients can come up in handy if you lot need to update your uncertainty budget. You lot can simply update the change in temperature (Ux).
Common Examples of Thermal Linear Expansion
Case one. Temperature change during exam/calibration
Ane of the nigh mutual sources of uncertainty for thermal linear expansion is the change in temperature during testing or scale.
Imagine that you are calibrating a caliper with a 1-inch stainless steel approximate block. When you begin the calibration, the temperature is 20 °C. When you finish the calibration, the temperature changed to twenty.2 °C.
Using the thermal linear expansion equation, yous find that the bodily length of your gauge block changed 2.2 micro-inches.
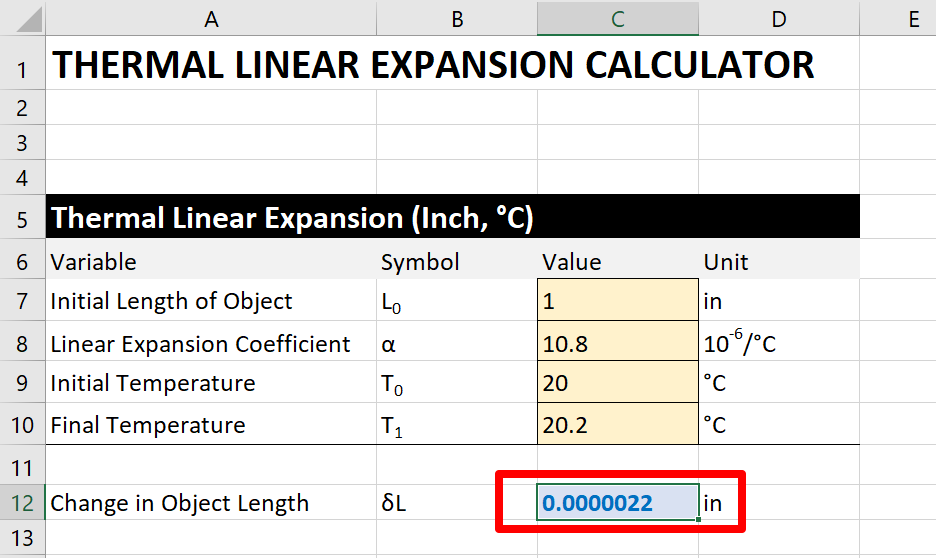
If you do not correct for this at the time of exam or scale, then you lot should consider adding this source of uncertainty in your uncertainty budget.
Case two. Temperature deviation between utilize and final scale
Another mutual source of incertitude for thermal linear expansion is the difference in temperature between the environment that an detail is calibrated in versus the environment where it is used.
Imagine that you are calibrating a caliper with a one-inch stainless steel gauge block. When you perform the calibration, the temperature is 21 °C. Nonetheless, the judge block was calibrated at 20 °C.
Using the thermal linear expansion equation, you find that the actual length of your approximate block changed 10.eight micro-inches.
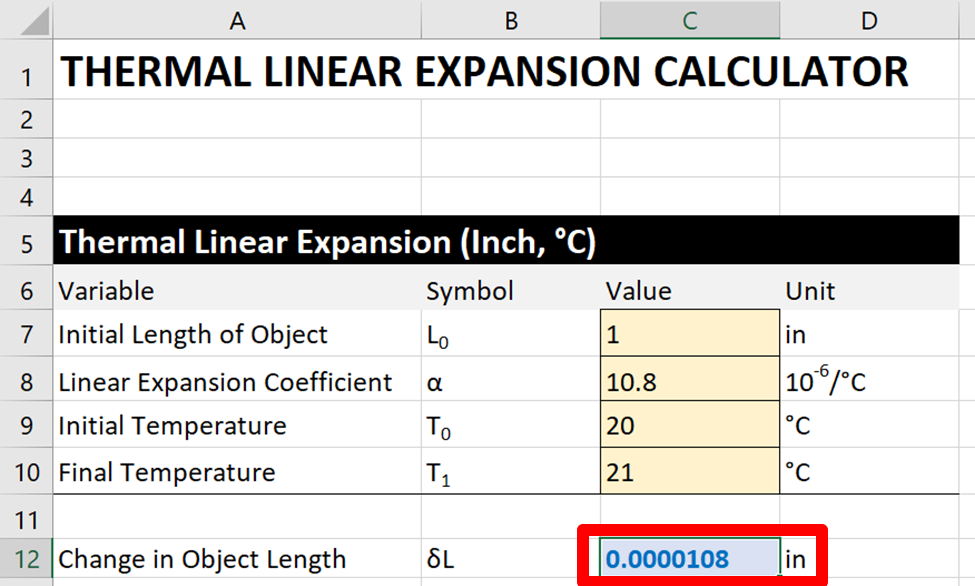
If you exercise not correct for this at the time of test or calibration, then you should consider adding this source of uncertainty in your uncertainty upkeep.
Conclusion
Thermal expansion tin can impact your measurement results. Information technology is a source of uncertainty that you should include in your uncertainty budgets if:
- Y'all perform dimensional or mechanical tests or calibration,
- Information technology's effect is meaning, and/or
- It's effect is non corrected for.
When tighter tolerances are required, meliorate quality measurements are important. Therefore, sources of measurement uncertainty, such as thermal expansion, need to be considered in your measurement results and minimized where practical.
In this guide, you should have learned the thermal linear expansion formula, how to calculate linear expansion, and how to include it in your uncertainty budgets.
Try adding it to your uncertainty budgets next fourth dimension and let me know how it afflicted your measurement results.
Click here to download the thermal expansion calculator for free!
Source: https://www.isobudgets.com/how-to-calculate-linear-thermal-expansion-for-measurement-uncertainty/

0 Response to "How to Read Coefficient of Linear Expansion"
Post a Comment